[NOIP 2002 普及组] 过河卒

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0, 0)、B 点 (n, m)，同样马的位置坐标是需要给出的。

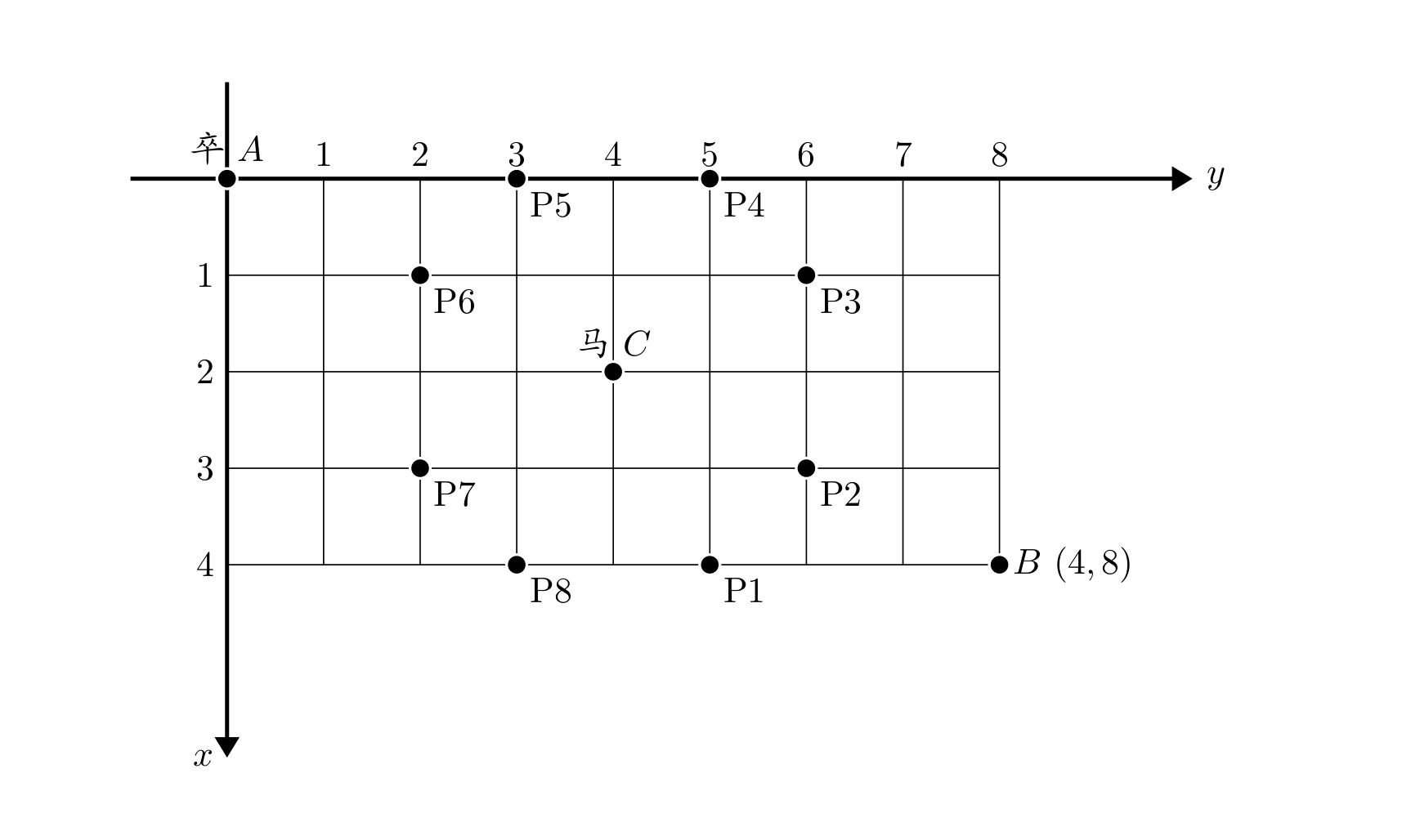
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

6 6 3 3

样例输出 #1

6

提示

对于100%的数据，1≤n,m≤20，1≤马的坐标≤20。

【题目来源】

NOIP 2002 普及组第四题

题解

60pts DFS

#include<iostream>
#include<cstdio>
#include<string>
#include<cmath>
#define MAXN 25
using namespace std;
int n,m;
long long ans;
int x,y;
bool mp[MAXN][MAXN];
int dx[5]={0,0,1};
int dy[5]={0,1,0};
bool been[MAXN][MAXN]; //防止重复遍历
int t;
void dfs(int xx,int yy){//深度优先搜索
	t++;
	if(xx==n&&yy==m){
		ans++;
		return ;
	}
	for(int i=1;i<=2;i++){
		int mx=xx+dx[i],my=yy+dy[i];
		if(!mp[mx][my]&&mx<=n&&my<=m){
			dfs(mx,my);
		}
	}
}
int main(){
	cin>>n>>m;
	cin>>x>>y;
	mp[x][y]=1;
	if(x-1>=0&&y-2>=0){
		mp[x-1][y-2]=1;
	}
	if(x-1>=0){
		mp[x-1][y+2]=1;
	}
	if(x-2>=0&&y-1>=0){
		mp[x-2][y-1]=1;
	}
	if(x-2>=0){
		mp[x-2][y+1]=1;
	}
	if(y-1>=0){
		mp[x+2][y-1]=1;
	}
	if(y-2>=0){
		mp[x+1][y-2]=1;
	}
	mp[x+1][y+2]=1;
	mp[x+2][y+1]=1;
	dfs(0,0);
	cout<<ans<<endl;
	return 0;
} 

100pts DP

#include <iostream>

using namespace std;

long long a[21][21];
bool b[21][21];

int main(){
	int c[3],x,y;
	cin>>x>>y>>c[1]>>c[2];
    if(x>=c[1]-1&&c[1]-1>=0&&y>=c[2]+2&&c[2]+2>=0){b[c[1]-1][c[2]+2]=1;}
	if(x>=c[1]+1&&c[1]+1>=0&&y>=c[2]+2&&c[2]+2>=0){b[c[1]+1][c[2]+2]=1;}
	if(x>=c[1]-2&&c[1]-2>=0&&y>=c[2]+1&&c[2]+1>=0){b[c[1]-2][c[2]+1]=1;}
	if(x>=c[1]+2&&c[1]+2>=0&&y>=c[2]+1&&c[2]+1>=0){b[c[1]+2][c[2]+1]=1;}
	if(x>=c[1]-2&&c[1]-2>=0&&y>=c[2]-1&&c[2]-1>=0){b[c[1]-2][c[2]-1]=1;}
	if(x>=c[1]+2&&c[1]+2>=0&&y>=c[2]-1&&c[2]-1>=0){b[c[1]+2][c[2]-1]=1;}
	if(x>=c[1]-1&&c[1]-1>=0&&y>=c[2]-2&&c[2]-2>=0){b[c[1]-1][c[2]-2]=1;}
	if(x>=c[1]+1&&c[1]+1>=0&&y>=c[2]-2&&c[2]-2>=0){b[c[1]+1][c[2]-2]=1;}
	b[c[1]][c[2]]=1;
	a[0][0]=1,b[0][0]=1;
	for(int m=0;m<=x;m++){
		for(int mm=0;mm<=y;mm++){
			if(b[m][mm]==0){
			    if(m==0){
				    a[m][mm]=a[m][mm-1];
			    }
			    else if(mm==0){
				    a[m][mm]=a[m-1][mm];
			    }
			    else{
				    a[m][mm]=a[m-1][mm]+a[m][mm-1];
			    }
		    }
		}
	}
	cout<<a[x][y]<<endl;
	return 0;
}

其他页面